SECCON 2017 Online CTF writeup
SECCON2017のオンライン予選に参加したのでそのwriteupです。結果は700ptで321位。頑張らねば・・・。
Vigenere3d (crypto 100)
$ python Vigenere3d.py SECCON{**************************} **************
POR4dnyTLHBfwbxAAZhe}}ocZR3Cxcftw9
出力結果が上の暗号文になるような平文を探せという問題。まずタイトルからヴィジュネル暗号を使っていると分かります。 平文の一部が分かっているので、それと暗号文の情報から鍵を計算するスクリプトを書きました。
実行すると、鍵の一部が分かります。
$ ./search_key.py
plain: SECCON{**************************}
key: _KP2Za_**************************a
crypt: POR4dnyTLHBfwbxAAZhe}}ocZR3Cxcftw9
鍵長は14ですが、ここで与えられた暗号化スクリプトの15行目をみると、鍵の8~14文字目は1~7文字目を反転したものであると分かるので、鍵は以下のようになります。
key: _KP2Za__aZ2PK_
鍵が割り出せたので、暗号文と鍵の情報から平文を計算するスクリプトを書きます。
実行すればflagが出ます。
$ ./decrypt.py
POR4dnyTLHBfwbxAAZhe}}ocZR3Cxcftw9
_KP2Za__aZ2PK__KP2Za__aZ2PK__KP2Za
SECCON{Welc0me_to_SECCON_CTF_2017}
flag:
SECCON{Welc0me_to_SECCON_CTF_2017}
Run Me! (programming 100)
単純に実行すればflagが出そうですが、実際は再帰が深すぎてうまくいきません。みるからにフィボナッチ数列のプログラムなので、再帰を使わない方法で実装します。
実行すればflagが出ます。
$ ./Run_Me2.py
SECCON{65076140832331717667772761541872}
flag:
SECCON{65076140832331717667772761541872}
putchar music (programming 100)
見やすく整形し、コンパイルが通るように書き直します。
$ gcc ./putchar_music2.c -lm $ ./a.out > output.wav $ aplay output.wav
あの有名な曲が流れてきます。
flag:
SECCON{STAR_WARS}
SHA-1 is dead (crypto 100)
SHA-1が衝突する2つのファイルを探す問題。条件として2つのファイルは2017KiB以上2018KiB以下である必要があります。SHA-1は既にGoogleなどによって衝突が発見されており、同じハッシュ値を持った内容の異なるファイルが公開されています。SHA-1の仕組み上、この2つのファイルの末尾に同じデータを追加してもこれらのハッシュ値は変わらないので、それを使っていい感じにファイルサイズを調整します。
$ ./sha-1_is_dead.py SHA-1 hash file1: 108fa3cd125fbf1b14f05fef51fca3a0a12f1c97 file2: 108fa3cd125fbf1b14f05fef51fca3a0a12f1c97 $ ls file1 sha-1_is_dead.py shattered-2.pdf file2 shattered-1.pdf $
出来たファイルをsubmitしてflagを得ます。
flag:
SECCON{SHA-1_1995-2017?}
Log Search (web 100)
WebサーバのアクセスログをElastic searchで検索できるサービスが与えられます。検索窓にSQLインジェクションやXSSなど試してもSomething wrong... X(というメッセージが出てくるだけで対策されているっぽいので、適当にflagで検索してステータスが200になっているログを探してアクセスしたらflagが出てきました。
http://logsearch.pwn.seccon.jp//flag-b5SFKDJicSJdf6R5Dvaf2Tx5r4jWzJTX.txt
flag:
SECCON{N0SQL_1njection_for_Elasticsearch!}
おそらくもっとちゃんとした解き方があると思いますが想定解が分かりません。
JPEG file (binary 100)
壊れたjpegファイルが与えられます。ファイル中のどこか1bit修正すれば表示できるようになるらしいです。試しにGIMPで開こうとすると以下のメッセージが出ました。
Corrupt JPEG data: premature end of data segment Unsupported marker type 0xfc
よって画像ファイル中から0xfcとなっている箇所を探して修正すれば良いと分かります。JPEGでは、0xffの後にマーカータイプが来るので、0xfffcを探します。
$ hexdump -C problem.jpeg | grep 'ff fc' $
ところが上のコマンドを実行しても何も出てきませんでした。調べたところ、hexdumpの出力がちょうど0xffと0xfcの間で改行が入っていることが原因でした。次のスクリプトを実行してファイルを修正します。
ちゃんと画像が表示されてflagをゲット出来ました。

flag:
SECCON{jp3g_study}
Thank you for playing!
flag:
SECCON{We have done all the challenges. Enjoy last 12 hours. Thank you!}
pwn解いていない&100点問題しか解いてないので来年までに強くなってもっと高い点数を取れるようにしたいです。
Pythonでニューラルネットを実装する
「Pythonで多層パーセプトロンを実装する」では、多層パーセプトロンによってXOR関数を近似しましたが、重みや閾値などのパラメータは自分で決めていました。そこで今回は誤差逆伝播法を使ったニューラルネットワークを実装することでパラメータを自動で学習させてみます。
パーセプトロンとの違い
パーセプトロンもニューラルネットワークも脳の神経細胞が行う情報処理の仕組みを模倣したものであることは同じですが、ニューラルネットワークには以下のようなパーセプトロンとは異なる特徴があります。
特徴
- 出力が2値でない
- 活性化関数がステップ関数でない
- 損失関数
活性化関数
パーセプトロンでは、ニューロンが発火するかどうかは閾値によって決められ、出力される値は
か
のどちらかでした。しかしニューラルネットワークでは活性化関数というものを導入することでより複雑な発火の表現ができるようになっています。つまり活性化関数はニューロンがどのように発火するかを決めている関数といえます。活性化関数には種類があり、代表的なものでは以下の3種類があります。
シグモイド関数
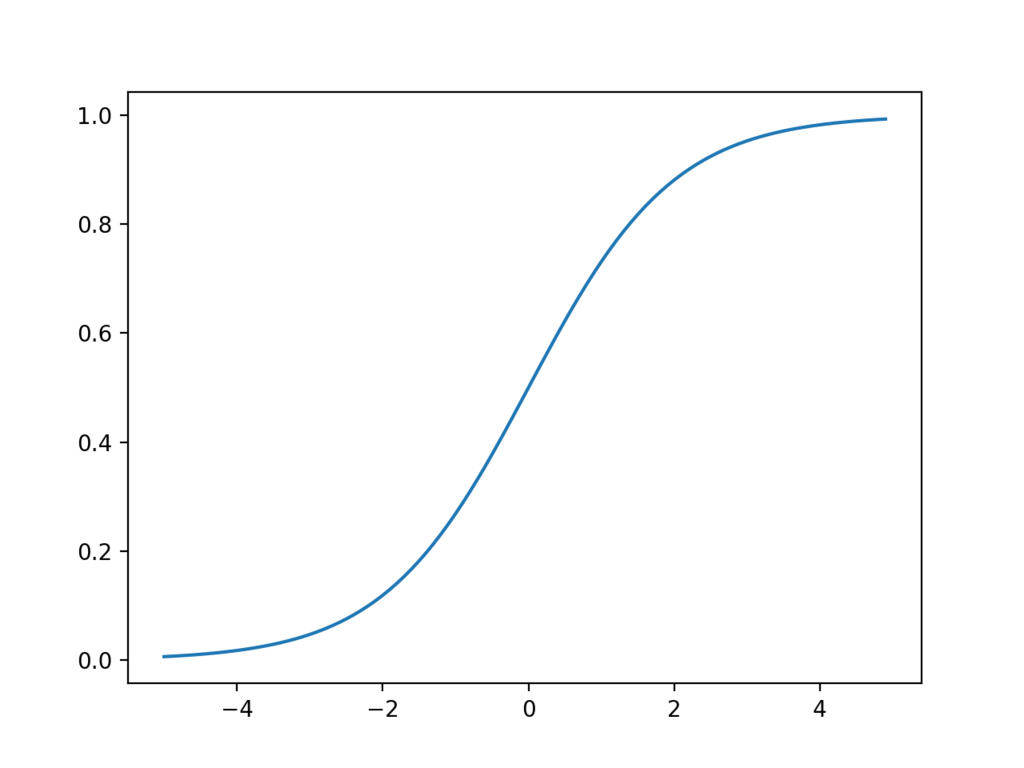
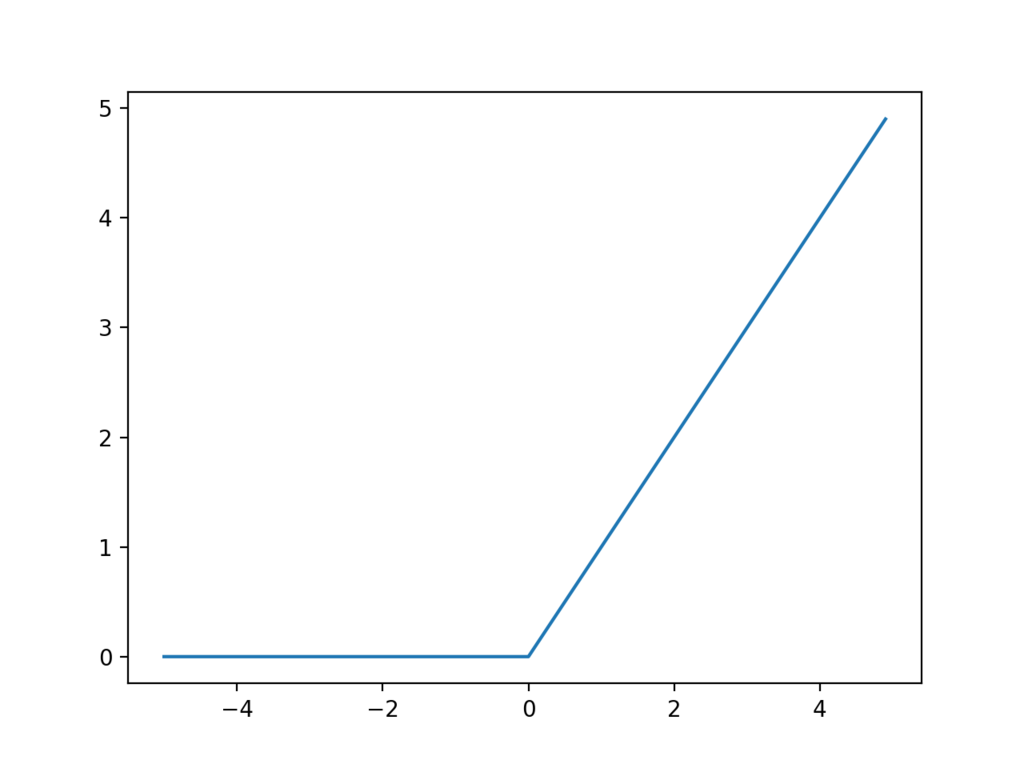
ReLU関数
tanh
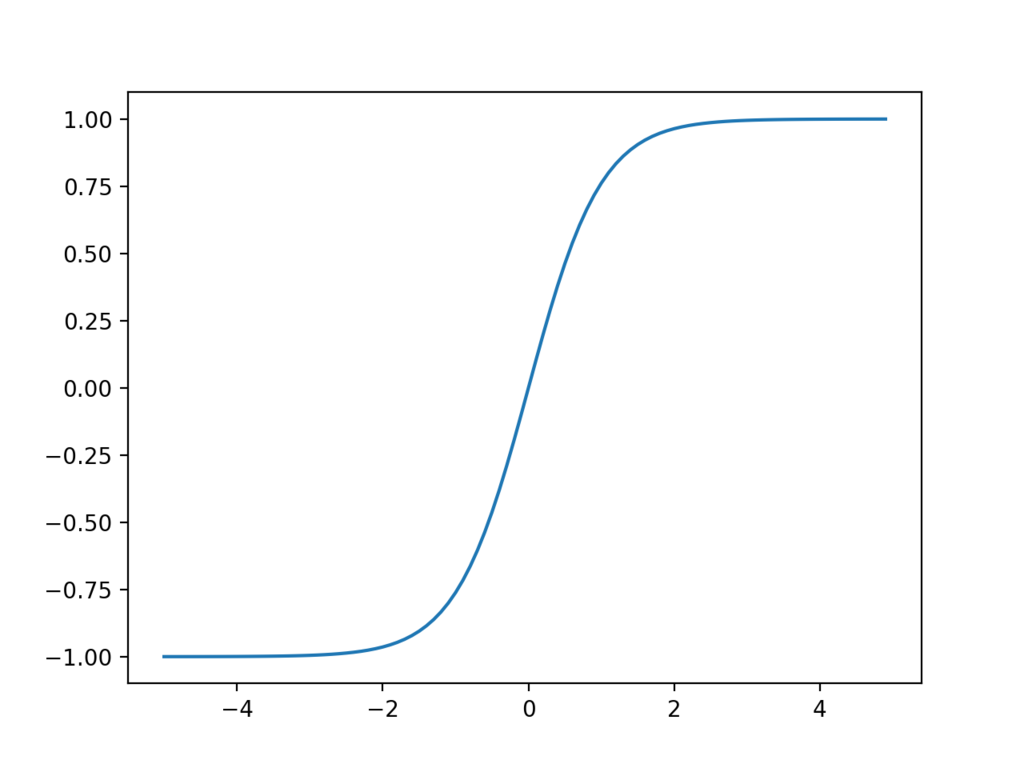
シグモイド関数やReLUは微分計算が簡単であることから広く使われています。tanhはRNNやLSTMなどの再帰型ニューラルネットによく使われます。
損失関数
損失関数とは、ニューラルネットワークの出力が正解データからどれだけ離れているか(誤差)を計算する関数です。一般的に回帰問題では2乗和誤差、分類問題ではクロスエントロピー誤差が用いられます。
2乗和誤差
クロスエントロピー誤差
ニューラルネットワークの順伝播
ニューラルネットを実装するにあたり、まず順伝播の計算式を導出します。今回は以下のような構造のネットワークを考えます。
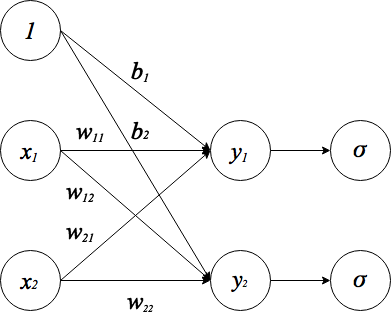
順伝播の流れを分かりやすくするために活性化関数()を明示的に書きました。
は入力信号、
は重み、
は出力信号を表しています。
はバイアスと呼ばれるもので、入力信号
と重み
をかけたものにこのバイアスを加えることで前回のエントリでいう閾値
と同じ役割を果たします。図では、バイアス項を加える処理を、入力
に
をかけるという処理で表しています。以上のことを踏まえると、まず活性化関数の手前までの計算は次のように表せます。
バイアス項が加わっただけで後はパーセプトロンの計算と変わりありません。 また、上の式はベクトルと行列を用いて一つの式にまとめることが出来ます。
ベクトルや行列を使って表すことで、プログラムに落とし込むときに線形代数のライブラリを活用でき、さらに一つの式にまとめることで入力や出力の数がどんなに多くなっても一層分の順伝播の計算は一回の計算で行えるようになります。ここで、
とすれば、上の式は
と非常に簡単な式になります。この計算は線形変換と呼ばれます。よって活性化関数を含めたこのニューラルネットワーク全体の順伝播の式は、
となります。さらに学習時には上の出力が損失関数に入力として与えられ、例えば2乗誤差を使う場合、
が誤差として出てきます。そしてこの誤差
から各パラメータ(重みやバイアスなど)に対する微分を効率的に計算するアルゴリズムが次に説明する誤差逆伝播法です。
誤差逆伝播法
ニューラルネットワークを学習させるにあたり、ニューラルネットワークが出力した誤差をもとに各パラメータをどれだけ修正するかを求める必要があります。この修正量は「あるパラメータを一定量変化させたときの誤差の変化量」と言い換えることができ、それは誤差に対する各パラメータの微分で表せます。この微分値を効率良く計算するアルゴリズムが誤差逆伝播法で、その原理の基本は連鎖律によって説明できます。
では上の順伝播計算で得た誤差から、学習すべきパラメータの誤差に対する微分を求めてみます。誤差逆伝播法では、出力層から逆順に誤差が伝播していくため、今回のネットワーク構造の場合は損失関数 -> 活性化関数 -> 線形変換の順に誤差が伝わっていきます。
損失関数の逆伝播
損失関数では学習するパラメータはありませんが後ろの層に誤差を伝えるため、を計算する必要があります。今回は損失関数に2乗和誤差を用いるので
は以下のようにして求められます。
これと順伝播の式を合わせて損失関数をPythonで書いてみます。
活性化関数の逆伝播
活性化関数についても同様に、学習すべきパラメータは無いので単純に誤差を入力信号で微分して後ろの層へ伝播させるだけです。今回はシグモイド関数とReLUを使います。まずシグモイド関数を微分してみると、
まとめると、
と導関数をシグモイド関数自身で表せます。これは重要な性質で、微分の計算をするときに順伝播で求めた値を再利用できるということです。Pythonによるシグモイド関数の実装は以下のようになります。
次にReLUの逆伝播を考えます。ReLUの微分はとても簡単です。
Pythonでの実装はこちらのリポジトリが参考になりました。
線形変換の逆伝播
線形変換では、重みとバイアス
の2つの学習パラメータがあります。そのため
,
を求めます。当然後ろの層へ誤差を伝えるために
も求めます。
また、微分の計算を分かりやすくするために、図のように線形変換を計算グラフで表します。
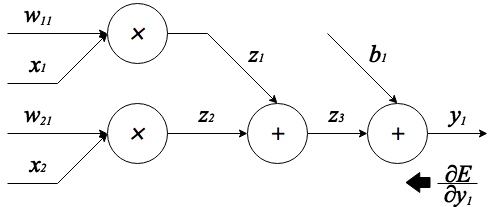
上の図は式 を表しています。さらに、上の式の計算途中の中間値を以下のように保存しておきます。
まず例として、出力から逆にたどって誤差に対する成分の微分を計算します。すると
は連鎖律を用いて、
と書けます。ここで、加算の部分は前の層から伝わってきた誤差をそのまま次の層に渡し、乗算の部分は入力信号をひっくり返したものを伝播させるので、
となります。他の成分も同様に誤差に対する微分を求めると、
となります。
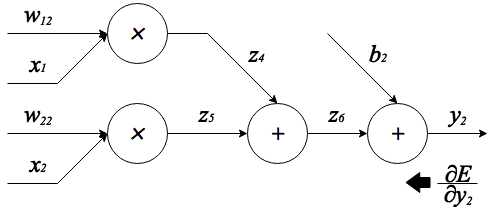
また、上の計算グラフは式 を表しており、計算途中の値は以下のように保存します。
これも先ほどと同様に誤差に対する各成分の微分を求めると、
これで誤差に対する全ての成分の微分が計算出来たのでそれらをまとめます。
すなわち、
したがってPythonでの実装は次のようになります。
勾配法
誤差逆伝播法によって各パラメータをどれだけ修正すれば良いか分かったので、次は実際にパラメータを調整してニューラルネットワークを学習させていきますが、その際に勾配法というアルゴリズムを使ってパラメータの値を更新していきます。勾配法(この場合は勾配降下法)では、損失関数の出力を最小にするために損失関数の勾配を活用します。具体的には、損失関数の勾配が小さくなる方へ進むことで損失関数の最小値を探します。式で表すと以下のようになります。
パラメータの更新式
上が重みパラメータ、下がバイアスパラメータの更新を行う式です。式中のは学習率というもので、誤差逆伝播法で得た修正量をどれだけ反映するか(どれだけパラメータを更新するか)を調整する係数です。Pythonで実装すると、以下のようになります。
今回実装するネットワークでは学習パラメータが存在するのは線形変換の部分のみなのでシグモイド関数やReLUでは何もしません。
実装
実装するのに必要な式が一通り表せたので、いよいよPythonでニューラルネットを実装します。今回もXOR関数を学習させてみます。まず以下のようにニューラルネットを訓練するクラスを書きました。
nnetモジュールには今までに書いた線形変換や活性化関数などのクラスがまとめてあります。また、上の訓練クラスを使ってXORの学習を行うコードスニペットの一例を以下にのせます。
さらに、学習したモデルを使って推論を行うスクリプトを作成しました。
上のコードでニューラルネットワークを訓練した結果、以下のようにXOR関数をうまく学習できました。
$ ./xor_predict.py ./xor_sample_weight.pkl in: [ 0. 0.] -> out: 0 (0.00486784050737) in: [ 0. 1.] -> out: 1 (0.997805826021) in: [ 1. 0.] -> out: 1 (0.997805828447) in: [ 1. 1.] -> out: 0 (0.00486784050737) $
今回作ったプログラムは以下のリポジトリに置いてあります。 github.com
PythonでグローバルIPアドレスを取得する
最近グローバルIPアドレスを調べることが多くなったのでまとめておくことにする。
DynDNS
DynDNSは、ダイナミックDNSのサービスです。自分のグローバルIPアドレスを知りたい場合はここにアクセスします。返ってくる結果には余分な文字列が含まれるので少しだけ追加の処理を行う必要があります。
>>> import urllib2 as u >>> url = 'http://checkip.dyndns.com/' >>> res = u.urlopen(url) >>> html = res.read() >>> html '<html><head><title>Current IP Check</title></head><body>Current IP Address: xxx.xxx.xxx.xxx</body></html>\r\n' >>> html.split(':')[1].strip().rstrip('</body></html>\r\n') 'xxx.xxx.xxx.xxx' >>>
ieServer.Net
ieServer.NetもDynDNSと同様にダイナミックDNSを提供してくれるサービスで、無料で利用することが出来ます。http://ipcheck.ieserver.net/にアクセスすると自分のグローバルIPアドレスを教えてもらえます。
>>> import requests >>> url = 'http://ipcheck.ieserver.net/' >>> res = requests.get(url) >>> res.text u'xxx.xxx.xxx.xxx\n' >>> str(res.text.rstrip('\n')) 'xxx.xxx.xxx.xxx' >>>
IP address information
このWebサイトは接続してきたクライアントのIPアドレス、ホスト名や国名などの情報を表示してくれます。URLの末尾にipを付加するとIPアドレスのみが取得でき、jsonを付加するとIPアドレス以外の情報も含めた様々な情報をjson形式で取得できます。
>>> import requests >>> res = requests.get('http://inet-ip.info/ip') >>> res.text u'xxx.xxx.xxx.xxx' >>>
ifconfig.io
こちらもグローバルIPアドレスやその他のネットワーク情報を出力してくれるWebサイトです。ただし、純粋にIPアドレスの文字列のみを返して欲しい場合はUser-Agentにcurlを設定してあげる必要があります。
>>> import requests >>> headers = {'User-Agent': 'curl'} >>> res = requests.get('http://ifconfig.io/', headers=headers) >>> res.text u'xxx.xxx.xxx.xxx\n' >>> str(res.text.rstrip('\n')) 'xxx.xxx.xxx.xxx' >>>
その他
ipify.org
>>> import requests >>> res = requests.get('http://api.ipify.org/') >>> res.text u'xxx.xxx.xxx.xxx' >>>
ident.me
>>> import requests >>> res = requests.get('http://ident.me') >>> res.text u'xxx.xxx.xxx.xxx' >>>
icanhazip.com
>>> import requests >>> res = requests.get('http://icanhazip.com') >>> res.text u'xxx.xxx.xxx.xxx\n' >>>
trackip.net
>>> import requests >>> res = requests.get('http://www.trackip.net/ip') >>> res.text u'xxx.xxx.xxx.xxx' >>>
dnsomatic.com
>>> import requests >>> res = requests.get('http://myip.dnsomatic.com') >>> res.text u'xxx.xxx.xxx.xxx' >>>
ちなみにグローバルIPアドレスをプログラムから利用したりしない場合はわざわざPythonスクリプトにしなくてもcurlとか使った方が速いです。
Pythonで多層パーセプトロンを実装する
多層パーセプトロン(multilayer perceptron)は、任意の関数を近似できるアルゴリズムです。ニューラルネットワークやディープラーニングのアルゴリズムを理解する前段階として、今回はこの多層パーセプトロンをPythonで実装してみます。
多層パーセプトロンとは
多層パーセプトロンの前にまず単純なパーセプトロンについて理解しておく必要があります。 パーセプトロンは脳の神経細胞(ニューロン)をモデルとして作られています。
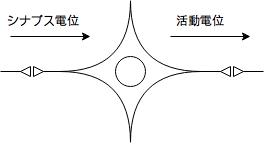
上に神経細胞の模式図を示しました。神経細胞は情報の伝達や処理を行うための細胞で、以下のような性質を持ちます。
- 多入力・多出力 : 複数の神経細胞から入力信号を受け、複数の神経細胞へ出力信号を送る。
- 情報の重み : 神経細胞間の結合強度によって情報が伝達される度合い(重み)が変わる。
- 発火 : 他の神経細胞から受け取った信号の総和がある閾値を超えると発火状態になり、信号を他の神経細胞に伝達する。
これらの性質を考慮して作られたモデルがパーセプトロンです。
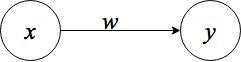
上図のように、入力信号を、出力信号を
、神経細胞同士の結合の度合いを
で表します。また、発火する際の閾値を
とします。入力信号
を受け取ると、パーセプトロンはその信号に重み
を掛け、その値が閾値
を超えた場合に
を出力し、そうでなければ
を出力します。式で表すと、
入力信号がつ以上の場合は、複数の入力信号の総和を計算し、閾値
と比較します。
パーセプトロンには、後述しますが直線(線形関数)しか近似できないという問題点があります。そこで直線だけでなく任意の関数を近似できるよう考案されたのが多層パーセプトロンです。多層パーセプトロンとは、入力層と出力層を含めて層の深さが以上のネットワークを指します。
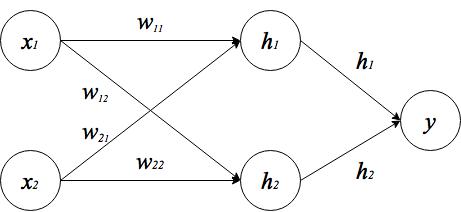
左から入力層、隠れ層、出力層となります。隠れ層を増やすことで表現力が増し、より複雑な関数を近似できます。
パーセプトロンの実装
試しにパーセプトロンにAND演算の機能を持たせてみましょう。AND演算の真理値表を以下に示します。
| 入力 |
入力 |
出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
この表から、AND演算をパーセプトロンで実現するにはつの信号を受け取って
つの信号を出力するようなパーセプトロンを用意すればいいことが分かります(下図)。
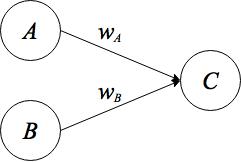
ただし、という信号を受け取ったとき
、それ以外の信号の組み合わせを受け取ったとき
を出力するような重み
、
と閾値
をパーセプトロンに設定してあげる必要があります。これらのパラメータは当てずっぽうで決めてもいいのですが、AND演算のグラフを使うとそれらのパラメータの設定を直感的に行えます。
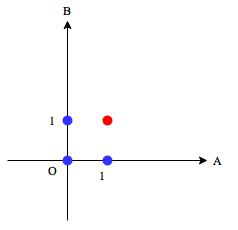
横軸は入力、縦軸は入力
です。また、出力
が
の点は赤色、
の点は青で表しています。このとき、青と赤の点を分離する直線を引けられればAND演算を実現できます。例えば、次の直線
はそのような条件を満たしています。
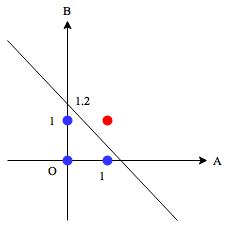
この直線の式を変形すると、
入力A、Bの係数はなので、この直線は入力A、Bにそれぞれ
の重みを掛けて足し合わせた値が閾値
を超えたかどうかを識別する関数を表していることが分かります。よってパーセプトロンがこの関数を近似するために設定すべきパラメータは、
となります。ではAND演算をPythonで実装してみます。
>>> def AND(A, B): ... W_a = 1 ... W_b = 1 ... theta = 1.2 ... out = W_a * A + W_b * B ... y = 1 if out > theta else 0 ... return y ... >>>
入力信号を与えてやると、
>>> AND(0, 0) 0 >>> AND(0, 1) 0 >>> AND(1, 0) 0 >>> AND(1, 1) 1 >>>
パーセプトロンでAND演算を実装できました。
多層パーセプトロンの実装
同じようにXOR演算をパーセプトロンで実装してみましょう。真理値表は以下の通りです。
| 入力 |
入力 |
出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
AND演算と同様にグラフを書くと、
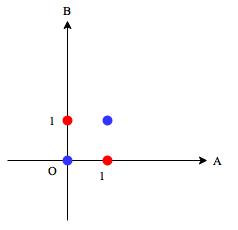
赤と青の点を一つの直線で分類できるでしょうか?XOR演算は、どのようなパラメータを与えても直線では分類出来ません(線形分離不可能)。パーセプトロンで近似できるのは線形の関数のみなので、非線形の関数も近似できる新たな仕組みが必要です。そこで先程説明した多層パーセプトロンを使います。
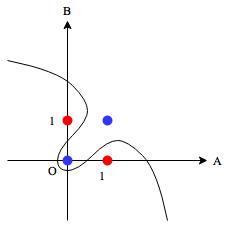
多層パーセプトロンを使えば上図のような曲線を近似させることが可能です。ただ、直線であれば重みや閾値を決めるのは簡単でも非線形のものではグラフを見てもパラメータを設定するのは困難です。そこでどうするかですが、結論を言ってしまうと既にパラメータが分かっているパーセプトロン(関数)を組み合わせるという方法があります。XORの場合は、
と表せることを利用します。OR演算やNAND演算は線形分離可能なのでAND演算と同じ方法でパラメータを決められます。これをパーセプトロンで表現すると、
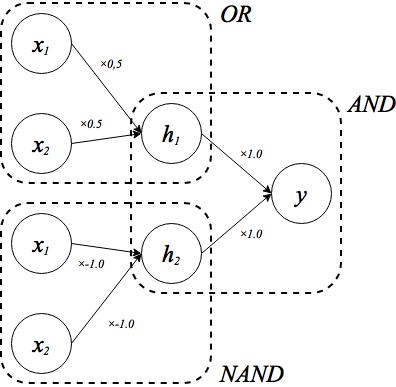
OR演算やNAND演算のパラメータの求め方はAND演算のときと同じなので省略しました。OR演算とNAND演算もそれぞれPythonで実装してみます。
>>> def OR(A, B): ... W_a = 0.5 ... W_b = 0.5 ... theta = 0.4 ... out = W_a * A + W_b * B ... y = 1 if out > theta else 0 ... return y ... >>> OR(0, 0), OR(0, 1), OR(1, 0), OR(1, 1) (0, 1, 1, 1) >>> >>> def NAND(A, B): ... W_a = -1.0 ... W_b = -1.0 ... theta = -1.2 ... out = W_a * A + W_b * B ... y = 1 if out > theta else 0 ... return y ... >>> NAND(0, 0), NAND(0, 1), NAND(1, 0), NAND(1, 1) (1, 1, 1, 0) >>>
パラメータを変えるだけで様々な機能を持たせられることが分かります。OR演算とNAND演算を呼び出した後にAND演算を呼び出せばいいので、XOR演算のコードは次のようになります。
>>> def XOR(A, B): ... h1 = OR(A, B) ... h2 = NAND(A, B) ... y = AND(h1, h2) ... return y ... >>> XOR(0, 0), XOR(0, 1), XOR(1, 0), XOR(1, 1) (0, 1, 1, 0) >>>
多層パーセプトロンを使って表現力を上げることでXOR演算を実装できました。
Hello World
ブログを始めました。 コンピュータ技術についての個人的なメモを書いていきたいと思っています。