Pythonで多層パーセプトロンを実装する
多層パーセプトロン(multilayer perceptron)は、任意の関数を近似できるアルゴリズムです。ニューラルネットワークやディープラーニングのアルゴリズムを理解する前段階として、今回はこの多層パーセプトロンをPythonで実装してみます。
多層パーセプトロンとは
多層パーセプトロンの前にまず単純なパーセプトロンについて理解しておく必要があります。 パーセプトロンは脳の神経細胞(ニューロン)をモデルとして作られています。
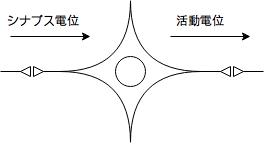
上に神経細胞の模式図を示しました。神経細胞は情報の伝達や処理を行うための細胞で、以下のような性質を持ちます。
- 多入力・多出力 : 複数の神経細胞から入力信号を受け、複数の神経細胞へ出力信号を送る。
- 情報の重み : 神経細胞間の結合強度によって情報が伝達される度合い(重み)が変わる。
- 発火 : 他の神経細胞から受け取った信号の総和がある閾値を超えると発火状態になり、信号を他の神経細胞に伝達する。
これらの性質を考慮して作られたモデルがパーセプトロンです。
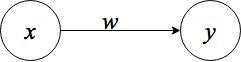
上図のように、入力信号を、出力信号を
、神経細胞同士の結合の度合いを
で表します。また、発火する際の閾値を
とします。入力信号
を受け取ると、パーセプトロンはその信号に重み
を掛け、その値が閾値
を超えた場合に
を出力し、そうでなければ
を出力します。式で表すと、
入力信号がつ以上の場合は、複数の入力信号の総和を計算し、閾値
と比較します。
パーセプトロンには、後述しますが直線(線形関数)しか近似できないという問題点があります。そこで直線だけでなく任意の関数を近似できるよう考案されたのが多層パーセプトロンです。多層パーセプトロンとは、入力層と出力層を含めて層の深さが以上のネットワークを指します。
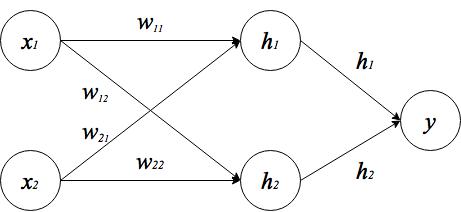
左から入力層、隠れ層、出力層となります。隠れ層を増やすことで表現力が増し、より複雑な関数を近似できます。
パーセプトロンの実装
試しにパーセプトロンにAND演算の機能を持たせてみましょう。AND演算の真理値表を以下に示します。
| 入力 |
入力 |
出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
この表から、AND演算をパーセプトロンで実現するにはつの信号を受け取って
つの信号を出力するようなパーセプトロンを用意すればいいことが分かります(下図)。
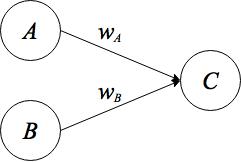
ただし、という信号を受け取ったとき
、それ以外の信号の組み合わせを受け取ったとき
を出力するような重み
、
と閾値
をパーセプトロンに設定してあげる必要があります。これらのパラメータは当てずっぽうで決めてもいいのですが、AND演算のグラフを使うとそれらのパラメータの設定を直感的に行えます。
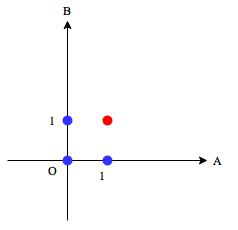
横軸は入力、縦軸は入力
です。また、出力
が
の点は赤色、
の点は青で表しています。このとき、青と赤の点を分離する直線を引けられればAND演算を実現できます。例えば、次の直線
はそのような条件を満たしています。
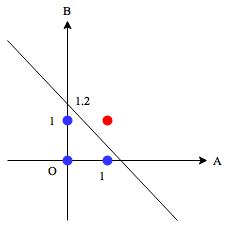
この直線の式を変形すると、
入力A、Bの係数はなので、この直線は入力A、Bにそれぞれ
の重みを掛けて足し合わせた値が閾値
を超えたかどうかを識別する関数を表していることが分かります。よってパーセプトロンがこの関数を近似するために設定すべきパラメータは、
となります。ではAND演算をPythonで実装してみます。
>>> def AND(A, B): ... W_a = 1 ... W_b = 1 ... theta = 1.2 ... out = W_a * A + W_b * B ... y = 1 if out > theta else 0 ... return y ... >>>
入力信号を与えてやると、
>>> AND(0, 0) 0 >>> AND(0, 1) 0 >>> AND(1, 0) 0 >>> AND(1, 1) 1 >>>
パーセプトロンでAND演算を実装できました。
多層パーセプトロンの実装
同じようにXOR演算をパーセプトロンで実装してみましょう。真理値表は以下の通りです。
| 入力 |
入力 |
出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
AND演算と同様にグラフを書くと、
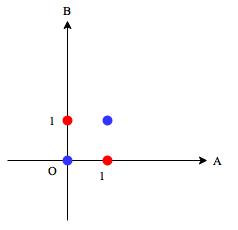
赤と青の点を一つの直線で分類できるでしょうか?XOR演算は、どのようなパラメータを与えても直線では分類出来ません(線形分離不可能)。パーセプトロンで近似できるのは線形の関数のみなので、非線形の関数も近似できる新たな仕組みが必要です。そこで先程説明した多層パーセプトロンを使います。
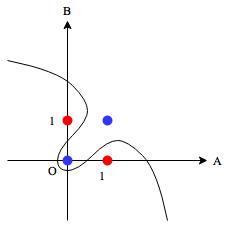
多層パーセプトロンを使えば上図のような曲線を近似させることが可能です。ただ、直線であれば重みや閾値を決めるのは簡単でも非線形のものではグラフを見てもパラメータを設定するのは困難です。そこでどうするかですが、結論を言ってしまうと既にパラメータが分かっているパーセプトロン(関数)を組み合わせるという方法があります。XORの場合は、
と表せることを利用します。OR演算やNAND演算は線形分離可能なのでAND演算と同じ方法でパラメータを決められます。これをパーセプトロンで表現すると、
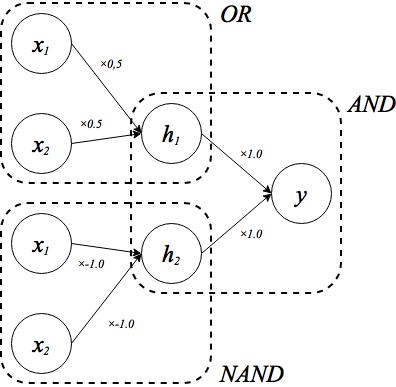
OR演算やNAND演算のパラメータの求め方はAND演算のときと同じなので省略しました。OR演算とNAND演算もそれぞれPythonで実装してみます。
>>> def OR(A, B): ... W_a = 0.5 ... W_b = 0.5 ... theta = 0.4 ... out = W_a * A + W_b * B ... y = 1 if out > theta else 0 ... return y ... >>> OR(0, 0), OR(0, 1), OR(1, 0), OR(1, 1) (0, 1, 1, 1) >>> >>> def NAND(A, B): ... W_a = -1.0 ... W_b = -1.0 ... theta = -1.2 ... out = W_a * A + W_b * B ... y = 1 if out > theta else 0 ... return y ... >>> NAND(0, 0), NAND(0, 1), NAND(1, 0), NAND(1, 1) (1, 1, 1, 0) >>>
パラメータを変えるだけで様々な機能を持たせられることが分かります。OR演算とNAND演算を呼び出した後にAND演算を呼び出せばいいので、XOR演算のコードは次のようになります。
>>> def XOR(A, B): ... h1 = OR(A, B) ... h2 = NAND(A, B) ... y = AND(h1, h2) ... return y ... >>> XOR(0, 0), XOR(0, 1), XOR(1, 0), XOR(1, 1) (0, 1, 1, 0) >>>
多層パーセプトロンを使って表現力を上げることでXOR演算を実装できました。
Hello World
ブログを始めました。 コンピュータ技術についての個人的なメモを書いていきたいと思っています。