Pythonでニューラルネットを実装する

「Pythonで多層パーセプトロンを実装する」では、多層パーセプトロンによってXOR関数を近似しましたが、重みや閾値などのパラメータは自分で決めていました。そこで今回は誤差逆伝播法を使ったニューラルネットワークを実装することでパラメータを自動で学習させてみます。

パーセプトロンとの違い

パーセプトロンもニューラルネットワークも脳の神経細胞が行う情報処理の仕組みを模倣したものであることは同じですが、ニューラルネットワークには以下のようなパーセプトロンとは異なる特徴があります。

特徴

出力が2値でない
活性化関数がステップ関数でない
損失関数

活性化関数

パーセプトロンでは、ニューロンが発火するかどうかは閾値 $\textstyle \theta$ によって決められ、出力される値は $\textstyle 0$ か $\textstyle 1$ のどちらかでした。しかしニューラルネットワークでは活性化関数というものを導入することでより複雑な発火の表現ができるようになっています。つまり活性化関数はニューロンがどのように発火するかを決めている関数といえます。活性化関数には種類があり、代表的なものでは以下の3種類があります。

シグモイド関数

$f(x) = \dfrac{1}{1 + \exp(-x)}$

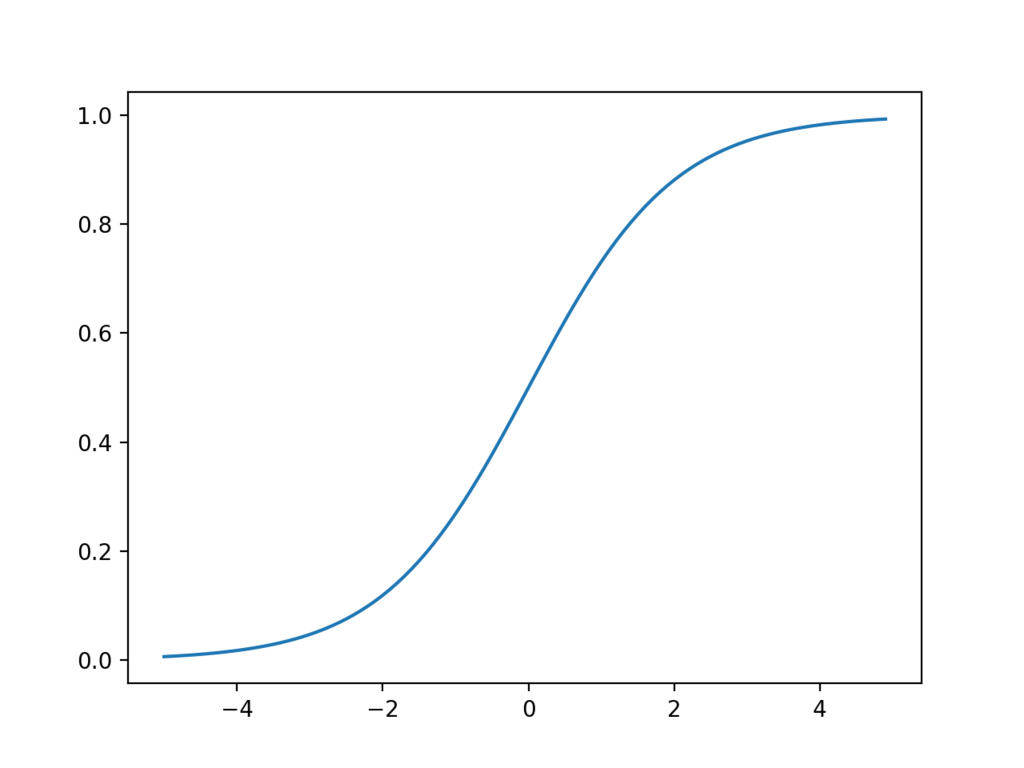
ReLU関数

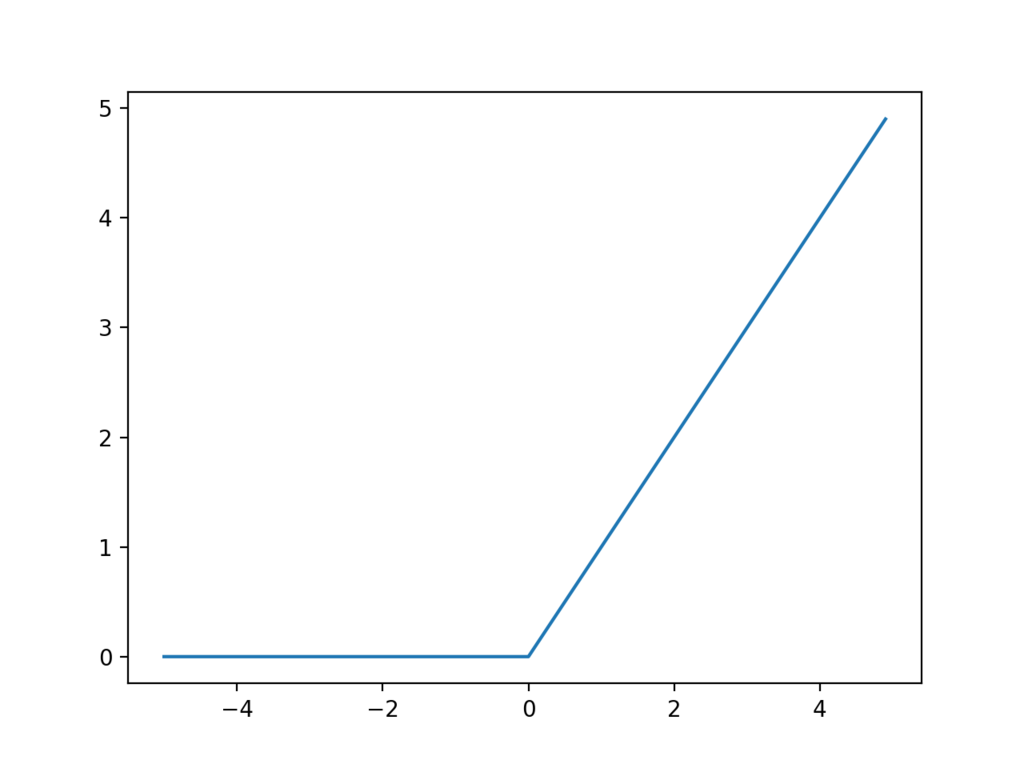
$f(x) = \left\{ \begin{array}{1} x \hspace{1em} ( x > 0 ) \\ 0 \hspace{1em} ( x \leqq 0 ) \end{array} \right.$

tanh

$f(x) = \tanh(x)$

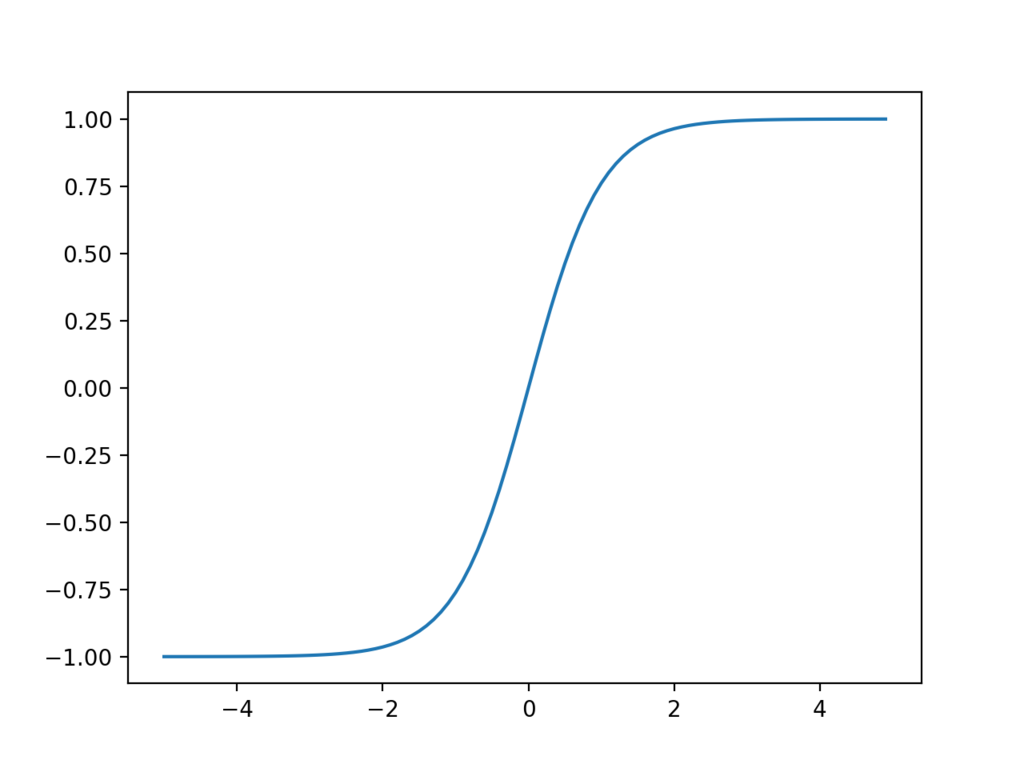
シグモイド関数やReLUは微分計算が簡単であることから広く使われています。tanhはRNNやLSTMなどの再帰型ニューラルネットによく使われます。

損失関数

損失関数とは、ニューラルネットワークの出力が正解データからどれだけ離れているか(誤差)を計算する関数です。一般的に回帰問題では2乗和誤差、分類問題ではクロスエントロピー誤差が用いられます。

2乗和誤差

$E = \displaystyle \frac{1}{2} \sum_{i} (y_i-t_i)^2$

クロスエントロピー誤差

$E = \displaystyle - \sum_{i} t_i \log y_i$

ニューラルネットワークの順伝播

ニューラルネットを実装するにあたり、まず順伝播の計算式を導出します。今回は以下のような構造のネットワークを考えます。

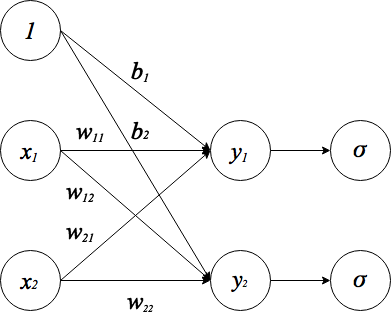
順伝播の流れを分かりやすくするために活性化関数( $\textstyle \sigma$ )を明示的に書きました。 $\textstyle x_i$ は入力信号、 $\textstyle w_{ij}$ は重み、 $\textstyle y_i$ は出力信号を表しています。 $\textstyle b_i$ はバイアスと呼ばれるもので、入力信号 $\textstyle x_i$ と重み $\textstyle w_{ij}$ をかけたものにこのバイアスを加えることで前回のエントリでいう閾値 $\textstyle \theta$ と同じ役割を果たします。図では、バイアス項を加える処理を、入力 $\textstyle 1$ に $\textstyle b_i$ をかけるという処理で表しています。以上のことを踏まえると、まず活性化関数の手前までの計算は次のように表せます。

$y_1 = x_1 w_{11} + x_2 w_{21} + b_1$

$y_2 = x_1 w_{12} + x_2 w_{22} + b_2$

バイアス項が加わっただけで後はパーセプトロンの計算と変わりありません。また、上の式はベクトルと行列を用いて一つの式にまとめることが出来ます。

$\displaystyle \begin{pmatrix} y_1 \quad y_2 \end{pmatrix} = \begin{pmatrix} x_1 \quad x_2 \end{pmatrix} \begin{pmatrix} w_{11} \quad w_{12} \\\ w_{21} \quad w_{22} \end{pmatrix} + \begin{pmatrix} b_1 \quad b_2 \end{pmatrix}$

ベクトルや行列を使って表すことで、プログラムに落とし込むときに線形代数のライブラリを活用でき、さらに一つの式にまとめることで入力や出力の数がどんなに多くなっても一層分の順伝播の計算は一回の計算で行えるようになります。ここで、

$\boldsymbol{Y} = \begin{pmatrix} y_1 \quad y_2 \end{pmatrix},\quad$ $\boldsymbol{X} = \begin{pmatrix} x_1 \quad x_2 \end{pmatrix},\quad$ $\boldsymbol{W} = \begin{pmatrix} w_{11} \quad w_{12} \\\ w_{21} \quad w_{22} \end{pmatrix},\quad$ $\boldsymbol{B} = \begin{pmatrix} b_1 \quad b_2 \end{pmatrix}$

とすれば、上の式は

$\boldsymbol{Y} = \boldsymbol{X} \cdot \boldsymbol{W} + \boldsymbol{B}$

と非常に簡単な式になります。この計算は線形変換と呼ばれます。よって活性化関数を含めたこのニューラルネットワーク全体の順伝播の式は、

$\boldsymbol{o} = \sigma \begin{pmatrix} \boldsymbol{Y} \end{pmatrix} = \sigma \begin{pmatrix} \boldsymbol{X} \cdot \boldsymbol{W} + \boldsymbol{B} \end{pmatrix}$

となります。さらに学習時には上の出力が損失関数に入力として与えられ、例えば2乗誤差を使う場合、

$\displaystyle E = \frac{1}{2}\sum_{i}(o_i - t_i)^2$

が誤差 $\textstyle E$ として出てきます。そしてこの誤差 $\textstyle E$ から各パラメータ(重みやバイアスなど)に対する微分を効率的に計算するアルゴリズムが次に説明する誤差逆伝播法です。

誤差逆伝播法

ニューラルネットワークを学習させるにあたり、ニューラルネットワークが出力した誤差をもとに各パラメータをどれだけ修正するかを求める必要があります。この修正量は「あるパラメータを一定量変化させたときの誤差の変化量」と言い換えることができ、それは誤差に対する各パラメータの微分で表せます。この微分値を効率良く計算するアルゴリズムが誤差逆伝播法で、その原理の基本は連鎖律によって説明できます。

では上の順伝播計算で得た誤差から、学習すべきパラメータの誤差に対する微分を求めてみます。誤差逆伝播法では、出力層から逆順に誤差が伝播していくため、今回のネットワーク構造の場合は損失関数 -> 活性化関数 -> 線形変換の順に誤差が伝わっていきます。

損失関数の逆伝播

損失関数では学習するパラメータはありませんが後ろの層に誤差を伝えるため、 $\textstyle \frac{\partial E}{\partial y}$ を計算する必要があります。今回は損失関数に2乗和誤差を用いるので $\textstyle \frac{\partial E}{\partial y}$ は以下のようにして求められます。

$\begin{eqnarray*} \dfrac{\partial E}{\partial y} &=& \displaystyle \dfrac{\partial}{\partial y} \begin{pmatrix} \dfrac{1}{2} \sum_{i}(y_i - t_i)^{2} \end{pmatrix} \\\ \\\ &=& 2 \cdot \dfrac{1}{2} \sum_{i}(y_i - t_i) \cdot (y_i - t_i)' \\\ \\\ &=& \sum_{i}(y_i - t_i) \end{eqnarray*}$

これと順伝播の式を合わせて損失関数をPythonで書いてみます。

活性化関数の逆伝播

活性化関数についても同様に、学習すべきパラメータは無いので単純に誤差を入力信号で微分して後ろの層へ伝播させるだけです。今回はシグモイド関数とReLUを使います。まずシグモイド関数を微分してみると、

$\begin{eqnarray*} \dfrac{d}{dx}f(x) &=& \dfrac{ -(1 + \exp(-x))' }{ (1 + \exp(-x))^{2} } \\\ \\\ &=& \dfrac{ \exp(-x) }{ (1 + \exp(-x))^{2} } \\\ \\\ &=& \dfrac{ 1 }{ 1 + \exp(-x) } \dfrac{ \exp(-x) }{ 1 + \exp(-x) } \\\ \\\ &=& \dfrac{ 1 }{ 1 + \exp(-x) } \dfrac{ 1 + \exp(-x) -1}{ 1 + \exp(-x) } \\\ \\\ &=& \dfrac{ 1 }{ 1 + \exp(-x) } \begin{pmatrix} 1 - \dfrac{ 1 }{ 1 + \exp(-x) } \end{pmatrix} \end{eqnarray*}$

まとめると、

$\dfrac{d}{dx}f(x) = f(x) (1 - f(x))$

と導関数をシグモイド関数自身で表せます。これは重要な性質で、微分の計算をするときに順伝播で求めた値を再利用できるということです。Pythonによるシグモイド関数の実装は以下のようになります。

次にReLUの逆伝播を考えます。ReLUの微分はとても簡単です。

${ \dfrac{d}{dx}f(x) = \left\{ \begin{array}{1} 1 \hspace{1em} ( x > 0 ) \\ 0 \hspace{1em} ( x \leqq 0 ) \end{array} \right. }$

Pythonでの実装はこちらのリポジトリが参考になりました。

線形変換の逆伝播

線形変換では、重み $\textstyle w_{ij}$ とバイアス $\textstyle b_{i}$ の2つの学習パラメータがあります。そのため $\tfrac{\partial E}{\partial \boldsymbol{W}}$ , $\tfrac{\partial E}{\partial \boldsymbol{B}}$ を求めます。当然後ろの層へ誤差を伝えるために $\tfrac{\partial E}{\partial \boldsymbol{X}}$ も求めます。

また、微分の計算を分かりやすくするために、図のように線形変換を計算グラフで表します。

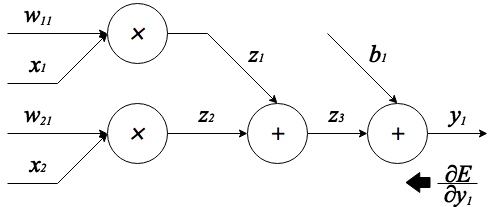
上の図は式 $\textstyle y_1 = x_1 w_{11} + x_2 w_{21} + b_1$ を表しています。さらに、上の式の計算途中の中間値を以下のように保存しておきます。

$z_1 = x_1 w_{11} , \quad z_2 = x_2 w_{21} , \quad z_3 = z_1 + z_2$

まず例として、出力から逆にたどって誤差に対する $x_1$ 成分の微分を計算します。すると $\tfrac{\partial E}{\partial x_1}$ は連鎖律を用いて、

$\dfrac{\partial E}{\partial x_1} = \dfrac{\partial E}{\partial z_3} \dfrac{\partial z_3}{\partial z_1} \dfrac{\partial z_1}{\partial x_1}$

と書けます。ここで、加算の部分は前の層から伝わってきた誤差をそのまま次の層に渡し、乗算の部分は入力信号をひっくり返したものを伝播させるので、

$\dfrac{\partial E}{\partial x_1} = \dfrac{\partial E}{\partial y_1} w_{11}$

となります。他の成分も同様に誤差に対する微分を求めると、

$\dfrac{\partial E}{\partial x_2} = \dfrac{\partial E}{\partial z_3} \dfrac{\partial z_3}{\partial z_2} \dfrac{\partial z_2}{\partial x_2} = \dfrac{\partial E}{\partial y_1} w_{21}$

$\dfrac{\partial E}{\partial w_{11}} = \dfrac{\partial E}{\partial z_3} \dfrac{\partial z_3}{\partial z_1} \dfrac{\partial z_1}{\partial w_{11}} = \dfrac{\partial E}{\partial y_1} x_1$

$\dfrac{\partial E}{\partial w_{21}} = \dfrac{\partial E}{\partial z_3} \dfrac{\partial z_3}{\partial z_2} \dfrac{\partial z_2}{\partial w_{21}} = \dfrac{\partial E}{\partial y_1} x_2$

$\dfrac{\partial E}{\partial b_1 } = \dfrac{\partial E}{\partial y_1}$

となります。

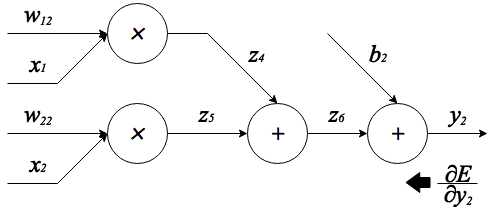
また、上の計算グラフは式 $\textstyle y_2 = x_1 w_{12} + x_2 w_{22} + b_2$ を表しており、計算途中の値は以下のように保存します。

$z_4 = x_1 w_{12} , \quad z_5 = x_2 w_{22} , \quad z_6 = z_4 + z_5$

これも先ほどと同様に誤差に対する各成分の微分を求めると、

$\dfrac{\partial E}{\partial x_1} = \dfrac{\partial E}{\partial z_6} \dfrac{\partial z_6}{\partial z_4} \dfrac{\partial z_4}{\partial x_1} = \dfrac{\partial E}{\partial y_2} w_{12}$

$\dfrac{\partial E}{\partial x_2} = \dfrac{\partial E}{\partial z_6} \dfrac{\partial z_6}{\partial z_5} \dfrac{\partial z_5}{\partial x_5} = \dfrac{\partial E}{\partial y_2} w_{22}$

$\dfrac{\partial E}{\partial w_{12}} = \dfrac{\partial E}{\partial z_6} \dfrac{\partial z_6}{\partial z_4} \dfrac{\partial z_4}{\partial w_{12}} = \dfrac{\partial E}{\partial y_2} x_1$

$\dfrac{\partial E}{\partial w_{22}} = \dfrac{\partial E}{\partial z_6} \dfrac{\partial z_6}{\partial z_5} \dfrac{\partial z_5}{\partial w_{22}} = \dfrac{\partial E}{\partial y_2} x_2$

$\dfrac{\partial E}{\partial b_2 } = \dfrac{\partial E}{\partial y_2}$

これで誤差に対する全ての成分の微分が計算出来たのでそれらをまとめます。

$\begin{eqnarray*} \dfrac{\partial E}{\partial \boldsymbol{X} } &=& \begin{pmatrix} \dfrac{\partial E}{\partial x_1} \quad \dfrac{\partial E}{\partial x_2} \end{pmatrix} \\\ &=& \begin{pmatrix} \dfrac{\partial E}{\partial y_1} w_{11} + \dfrac{\partial E}{\partial y_2} w_{12} \quad \dfrac{\partial E}{\partial y_1} w_{21} + \dfrac{\partial E}{\partial y_2} w_{22} \end{pmatrix} \\\ &=& \begin{pmatrix} \dfrac{\partial E}{\partial y_1} \quad \dfrac{\partial E}{\partial y_2} \end{pmatrix} \cdot \begin{pmatrix} w_{11} \quad w_{21} \\\ w_{12} \quad w_{22} \end{pmatrix} \\\ &=& \dfrac{\partial E}{\partial \boldsymbol{Y}} \cdot \boldsymbol{W}^T \end{eqnarray*}$

$\begin{eqnarray*} \dfrac{\partial E}{\partial \boldsymbol{W} } &=& \begin{pmatrix} \dfrac{\partial E}{\partial w_{11}} \quad \dfrac{\partial E}{\partial w_{21}} \\\ \dfrac{\partial E}{\partial w_{12}} \quad \dfrac{\partial E}{\partial w_{22}} \end{pmatrix} \\\ &=& \begin{pmatrix} \dfrac{\partial E}{\partial y_1} x_1 \quad \dfrac{\partial E}{\partial y_1} x_2 \\\ \dfrac{\partial E}{\partial y_2} x_1 \quad \dfrac{\partial E}{\partial y_2} x_2 \end{pmatrix} \\\ &=& \begin{pmatrix} x_1 \\\ x_2 \end{pmatrix} \cdot \begin{pmatrix} \dfrac{\partial E}{\partial y_1} \quad \dfrac{\partial E}{\partial y_2} \end{pmatrix} \\\ &=& \boldsymbol{X}^T \cdot \dfrac{\partial E}{\partial \boldsymbol{Y}} \end{eqnarray*}$ $\dfrac{\partial E}{\partial \boldsymbol{B} } = \begin{pmatrix} \dfrac{\partial E}{\partial b_1} \quad \dfrac{\partial E}{\partial b_2} \end{pmatrix} = \begin{pmatrix} \dfrac{\partial E}{\partial y_1} \quad \dfrac{\partial E}{\partial y_2} \end{pmatrix} = \dfrac{\partial E}{\partial \boldsymbol{Y}}$

すなわち、

$\dfrac{\partial E}{\partial \boldsymbol{W} } = \boldsymbol{X}^T \cdot \dfrac{\partial E}{\partial \boldsymbol{Y}}$

$\dfrac{\partial E}{\partial \boldsymbol{X} } = \dfrac{\partial E}{\partial \boldsymbol{Y}} \cdot \boldsymbol{W}^T$

$\dfrac{\partial E}{\partial \boldsymbol{B} } = \dfrac{\partial E}{\partial \boldsymbol{Y}}$

したがってPythonでの実装は次のようになります。

勾配法

誤差逆伝播法によって各パラメータをどれだけ修正すれば良いか分かったので、次は実際にパラメータを調整してニューラルネットワークを学習させていきますが、その際に勾配法というアルゴリズムを使ってパラメータの値を更新していきます。勾配法(この場合は勾配降下法)では、損失関数の出力を最小にするために損失関数の勾配を活用します。具体的には、損失関数の勾配が小さくなる方へ進むことで損失関数の最小値を探します。式で表すと以下のようになります。

パラメータの更新式

$\boldsymbol{W_{new}} = \boldsymbol{W_{old} } - \eta \dfrac{\partial E}{\partial \boldsymbol{W_{old}}}$

$\boldsymbol{B_{new}} = \boldsymbol{B_{old} } - \eta \dfrac{\partial E}{\partial \boldsymbol{B_{old}}}$

上が重みパラメータ、下がバイアスパラメータの更新を行う式です。式中の $\textstyle \eta$ は学習率というもので、誤差逆伝播法で得た修正量をどれだけ反映するか(どれだけパラメータを更新するか)を調整する係数です。Pythonで実装すると、以下のようになります。

今回実装するネットワークでは学習パラメータが存在するのは線形変換の部分のみなのでシグモイド関数やReLUでは何もしません。

実装

実装するのに必要な式が一通り表せたので、いよいよPythonでニューラルネットを実装します。今回もXOR関数を学習させてみます。まず以下のようにニューラルネットを訓練するクラスを書きました。

nnetモジュールには今までに書いた線形変換や活性化関数などのクラスがまとめてあります。また、上の訓練クラスを使ってXORの学習を行うコードスニペットの一例を以下にのせます。

さらに、学習したモデルを使って推論を行うスクリプトを作成しました。

上のコードでニューラルネットワークを訓練した結果、以下のようにXOR関数をうまく学習できました。

$ ./xor_predict.py ./xor_sample_weight.pkl
in: [ 0.  0.]  ->  out: 0 (0.00486784050737)
in: [ 0.  1.]  ->  out: 1 (0.997805826021)
in: [ 1.  0.]  ->  out: 1 (0.997805828447)
in: [ 1.  1.]  ->  out: 0 (0.00486784050737)
$

今回作ったプログラムは以下のリポジトリに置いてあります。 github.com